論文位置:https://arxiv.org/abs/2005.03448
Physics-informed learning of governing equations from scarce data
內容簡易翻譯
作者
陳鑷(Zhao Chen)1,*劉陽(Yang Liu)2,孫浩(Hao Sun)1,31 美國東北大學土木與環境工程系(波士頓) 2 美國東北大學機械與工業工程系(波士頓) 3 麻省理工學院土木與環境工程系(劍橋)
通訊作者信箱: [email protected]; [email protected]
摘要
利用數據揭示描述複雜物理系統行為的基本控制定律或方程,能顯著推動多學科領域的建模、模擬與理解。本文提出一種新型物理資訊深度學習架構(PiDL),用於從稀缺且含雜訊的資料中發現非線性時空系統的控制偏微分方程(PDE)。此方法深度融合了深度神經網路(DNN)的表示學習能力、物理嵌入、自動微分與稀疏迴歸技術,實現三大目標:
- 逼近系統變數解
- 計算關鍵導數項
- 辨識構成PDE結構與明確表達的關鍵導數項及參數
透過數值與實驗驗證,此方法在資料稀缺性和雜訊幹擾下對多種PDE系統(考慮不同初/邊值條件)的發現具有高效性與穩健性。該框架為實際應用中難以獲取大規模精確資料集的問題提供了閉式模型發現的潛力。
關鍵字:控制方程式發現、物理資訊深度學習、偏微分方程(PDE)
核心貢獻與重點
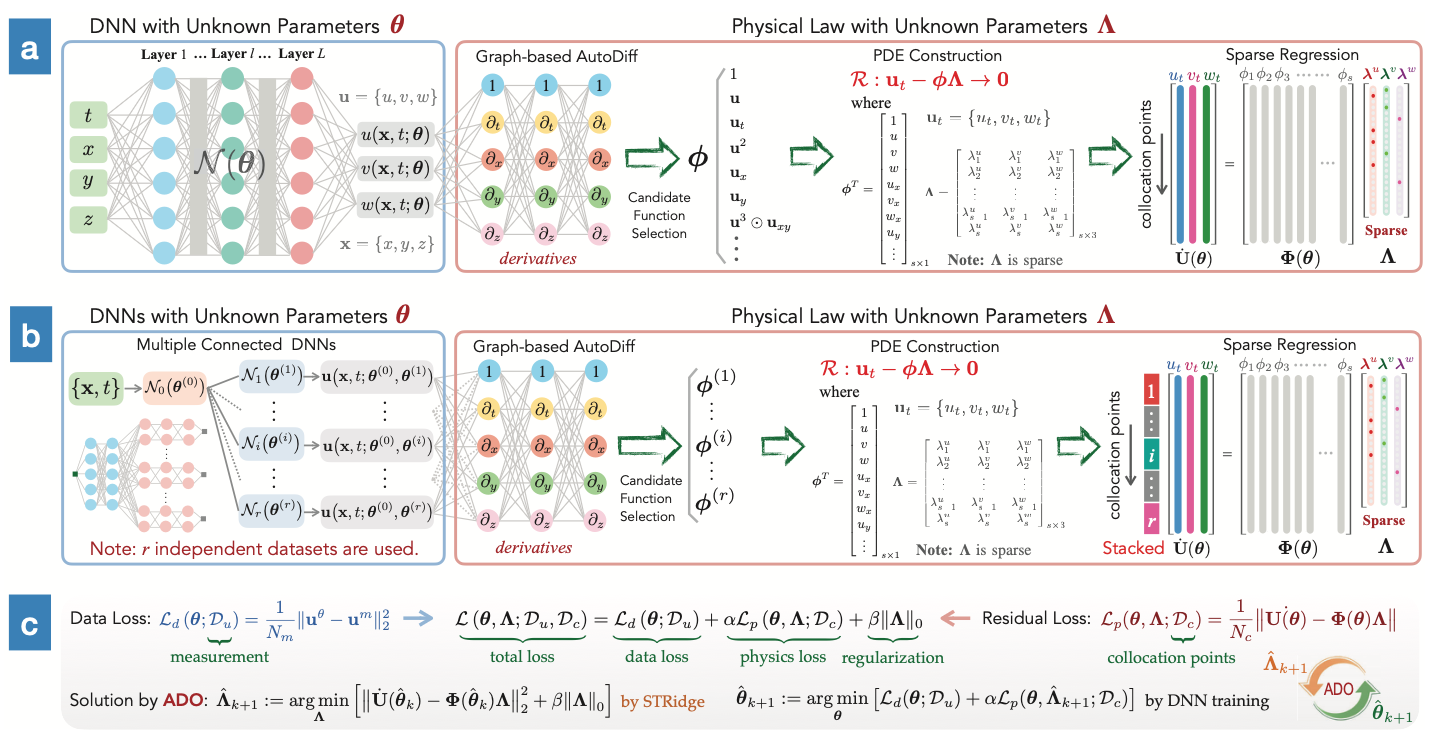
1. 問題背景
- 傳統PDE建模依賴第一原理(如守恆定律),但許多複雜系統的解析描述未知
- 資料驅動方法(如SINDy)受限於資料品質與數量,數值微分對雜訊敏感
2. PiDL框架創新
損失函數:
\mathcal{L}(\theta, \Lambda) = \underbrace{\mathcal{L}_d}_{\text{數據損失}} + \alpha \underbrace{\mathcal{L}_p}_{\text{物理損失}} + \beta \underbrace{\|\Lambda\|_0}_{\text{稀疏正則}}
技術融合:
- DNN學習系統解的表示
- 自動微分高精度計算導數
- ℓ₀稀疏迴歸辨識PDE關鍵項
網路架構:
- 單一資料集處理: └─ DNN直接建模解函數
- 多重資料集處理: └─ "根-分支"DNN結構處理不同初邊值條件 ├─ 共享根網路擷取共同特徵 └─ 獨立分支網路適應特定條件
最佳化演算法(ADO):
- 交替方向優化逐步訓練DNN參數(θ)與PDE係數(Λ)
- 解決ℓ₀正規的NP難問題
3. 實驗驗證
| PDE類型 | 雜訊等級 | 辨識誤差 | 資料使用量 |
|---|---|---|---|
| Burgers方程式 | 10% | 1.15% | 1.95% |
| KS方程式(混沌) | 10% | 0.71% | 12.3% |
| Navier-Stokes方程式 | 10% | 1.40% | 0.22% |
| Schrödinger方程式 | 10% | 2.31% | 37.5% |
多重資料集場景:
- Burgers方程式(小黏度衝擊波)
- Fitzhugh-Nagumo神經元模型
真實實驗: 細胞遷移增殖實驗發現Fisher-Kolmogorov模型:
\rho_t = \gamma \rho_{xx} + \lambda_1 \rho + \lambda_2 \rho^2